⌚ 2020/5/25 (Mon) 🔄 2024/3/20 (Wed)
【機械学習】基本的な手法の一つ!線形回帰を用いて、回帰直線を求めた実装について解説

線形回帰とは機械学習の手法として基本的な手法の一つです。
簡単な予測であれば、この手法を用いることで行うことができます。
この記事を読むと、
最小二乗法と勾配法を用いた場合の機械学習の手法
を学ぶことができます。
今回はそれぞれの手法を用いて、回帰直線を求めました。
機械学習の解説記事ではないので、細かい部分は省略していますがご了承ください。
機械学習について勉強するにあたっては、こちらの書籍を利用しました。
『夢見る機械学習 回帰・パーセプトロン[Python実装]入門』
-
機械学習の勉強を始めようと思っている方 -
線形回帰に興味のある方 -
分析手法を学びたい方
▼この記事を書いた人
サン・エム・システム㈱でアプリケーションエンジニアとして働いている ぽいう と言います。
雑食性の高い3年目のエンジニアです。
色々なことに挑戦したいと思っており、今回は機械学習に挑戦してみようと思いました。
そこで手始めに線形回帰のプログラムを作ってみました。
1. 線形回帰とは
線形回帰とは、データの分布があるときに、
そのデータに一番当てはまる直線を求める分析手法の一種です。
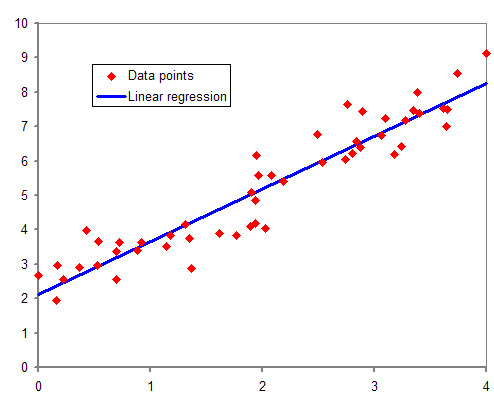
この記事では、下の画像のように2次元で表現できるデータを取り扱うので、
与えられたデータから y = ax + bの直線を求めることになります(画像は Wikipedia より)。
x のことを説明変数、y のことを目的変数と呼んだりします。
この直線を求めることによって、ある説明変数 x が与えられたとき、
相関のある目的変数 y を予測することができます。
相関とは、一方が増加するともう一方が増加/減少する関係のことです。
例えば、ストレージの利用日数が増加すると使用容量が増加する、といった感じです。
今回、線形回帰のプログラムを実装して、実際に弊社で運用中の DB サーバの容量が
いつ枯渇する(アラートが発生する)のかを予測してみました。
2. 使用する手法、データ
最小二乗法と勾配法を用いて、それぞれ回帰直線を求めてみました。
回帰直線を求めるデータの分布はこのようになっています。
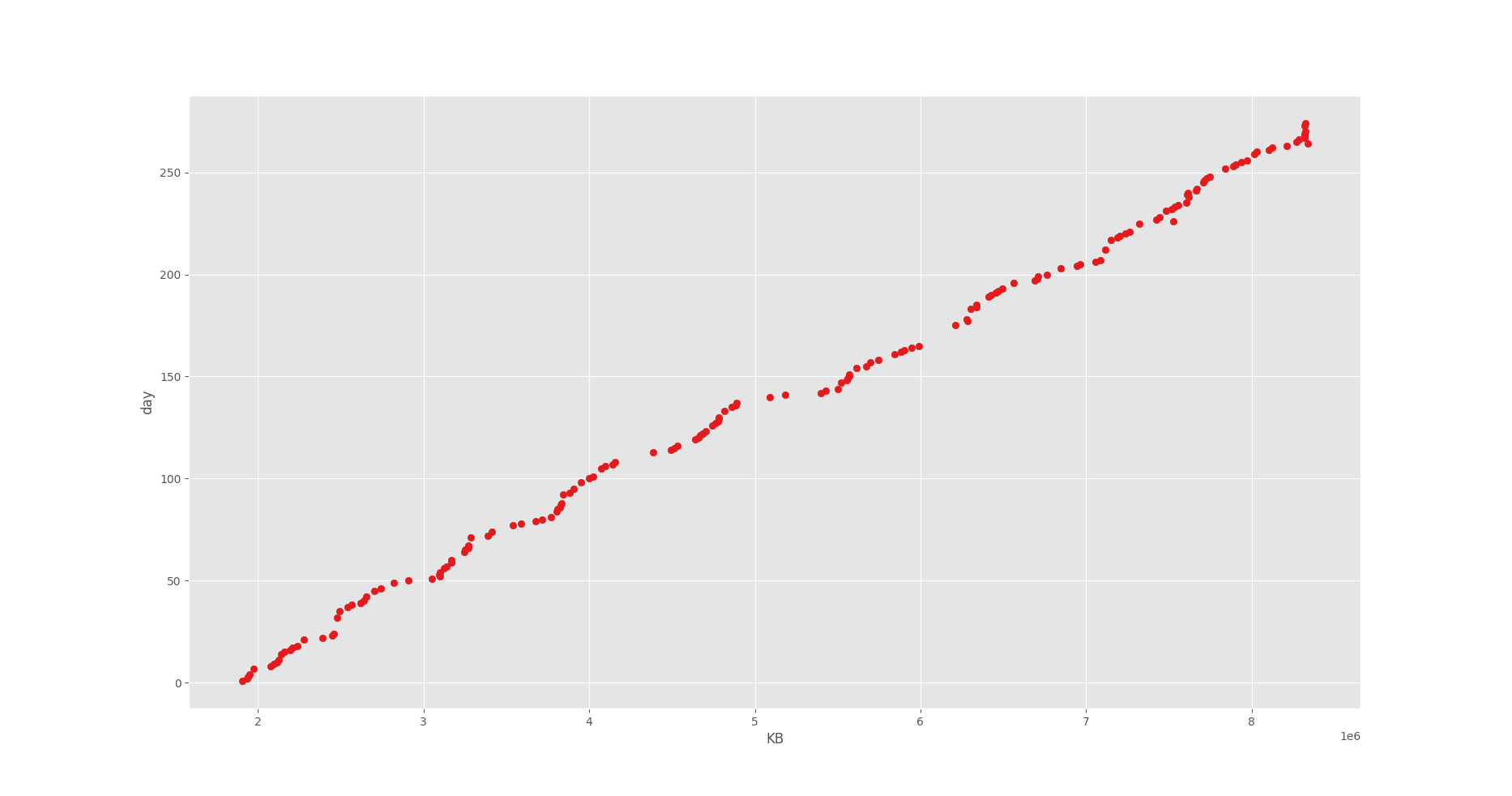
どうやら 8 GB ほど使用しているみたいですね(8 KB × 1e6)。
そして良い感じの相関があることが見て取れますね。
今回は枯渇する日付を求めたいので、このグラフの軸は下記のようになっています。
- x 軸:データ容量
- y 軸:計測日
3. 実装環境、使用したライブラリ
- python 3.8
- numpy 1.18.2
- pandas 1.0.3
- matplotlib 3.2.1
コードには一部ですが型ヒントを付けています。
型ヒントを付けるのが難しかったものは、docstring に記述しています。
4. 最小二乗法による実装
はじめに最小二乗法の実装です。
最小二乗法とは、ある直線 y = ax + b に対する誤差の二乗和を最小にすることで、
最も当てはまるパラメータ a, b を求める手法です。
下記画像の赤い破線の二乗の和が最小になるようなパラメータを求めます。
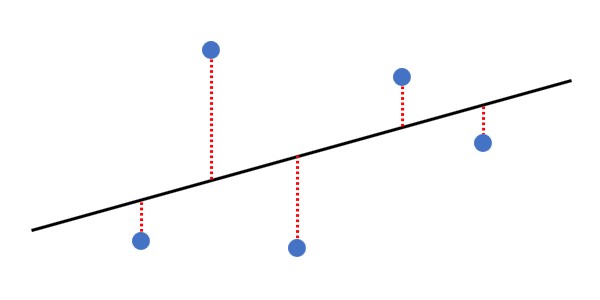
最小二乗法による回帰直線の求め方は割愛しますが、こちらが参考になるかと思います。
このサイトから抜粋すると、下記の数式を実装することで回帰直線を求めることができます。
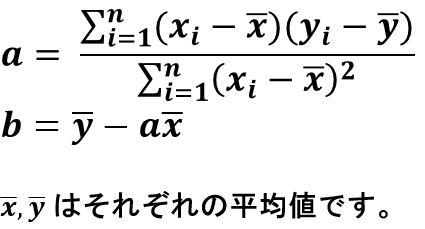
4-1. コード
インポートしている Excel ファイルには、
「計測日数」と「使用容量」というカラムがあるとします。
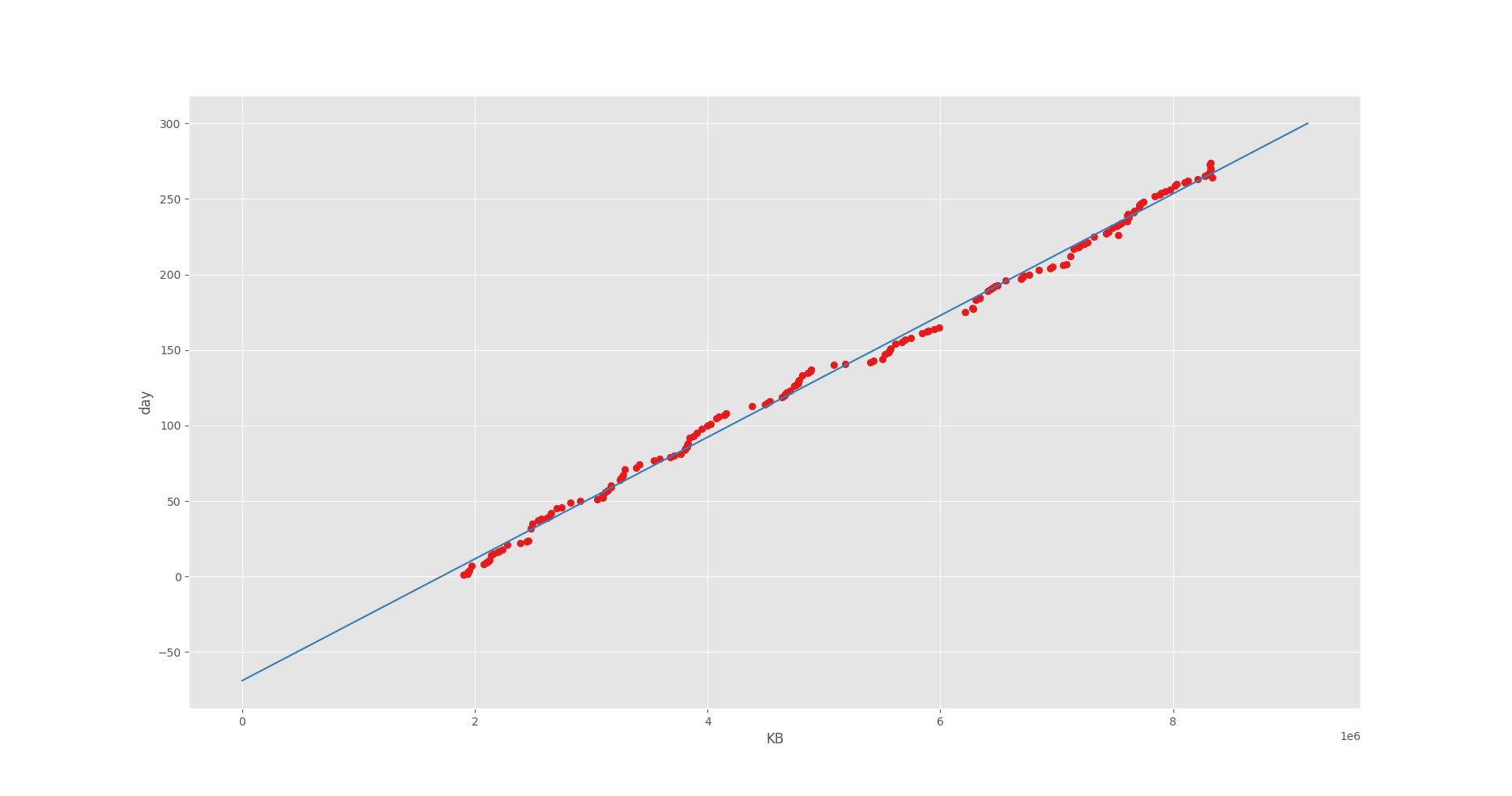
4-2. 結果
$ python least_square.py
アラート発生まであと 881 日
回帰直線がデータに沿って表⽰されていることが⾒て取れますね。
パラメータをうまく求めることができたようです。
5. 勾配法による実装
次に勾配法の実装です。
勾配法とは、繰り返しの計算によって近似的な値を求める⼿法です。
この⼿法で得られる近似解は、数値解と呼ばれます。
世の中には解析解を求めることができない問題が数多くあるそうです。
そのような問題を解くときに、この勾配法を利⽤します。
またしても細かい部分は割愛しますが、勾配法は下の図にあるように、
だんだんと最適な値へと近づいていきます。
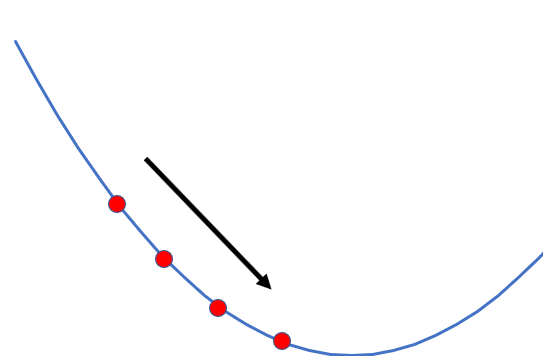
ここで重要になってくるのが、パラメータの更新です。
計算を繰り返すごとにパラメータを更新して、下記の数式の結果(誤差)が
最⼩になるようにします。
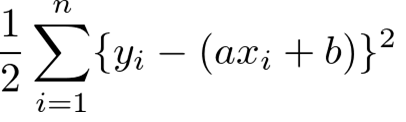
パラメータの更新回数は、⼀回前に求めた誤差との差分が⼗分に⼩さくなったら
終了するようにします。(この記事だと誤差の差分が以下になれば更新が終了します。)
パラメータの更新式は、求める回帰直線を
![]() とすると、下記になります。
とすると、下記になります。
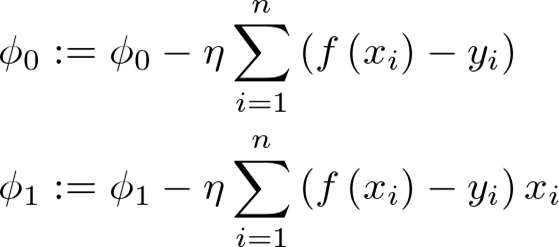
ここで現れる η は、学習率と呼ばれる正の定数です。
0.001 といった適当な小さな数字を利用します(この記事だと0.0001)。
だんだん機械学習っぽくなってきましたね。
また、ここで与える説明変数 x は標準化しておきます。
標準化されたデータは下記の数式を個々のデータに適用することによって得ることができます。
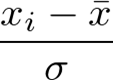
σ は x
の標準偏差です。
データを標準化することで、「平均=0、標準偏差=1」の分布にすることができます。
これによって、パラメータの更新が収束しやすくなります。
ちなみに今回標準化せずに学習した結果は、データの数値が大きすぎて発散してしまい、
まともな結果を得ることができませんでした。
データを標準化し、更新式を用いて学習することで回帰直線を求めることができます。
5-1. コード
こちらも同じデータを利用します。
5-2. 結果
$ python gradient.py
(1) Φ0: 3.204 Φ1: 2.006 diff: 70321.61080
(2) Φ0: 5.469 Φ1: 3.321 diff: 68020.14270
(3) Φ0: 7.696 Φ1: 4.615 diff: 65793.99647
(4) Φ0: 9.886 Φ1: 5.887 diff: 63640.70701
(5) Φ0: 12.041 Φ1: 7.139 diff: 61557.88986
(省略)
(610) Φ0: 140.443 Φ1: 81.729 diff: 0.00011
(611) Φ0: 140.443 Φ1: 81.729 diff: 0.00011
(612) Φ0: 140.443 Φ1: 81.729 diff: 0.00010
(613) Φ0: 140.443 Φ1: 81.729 diff: 0.00010
(614) Φ0: 140.443 Φ1: 81.729 diff: 0.00010
アラート発生まであと 881 日
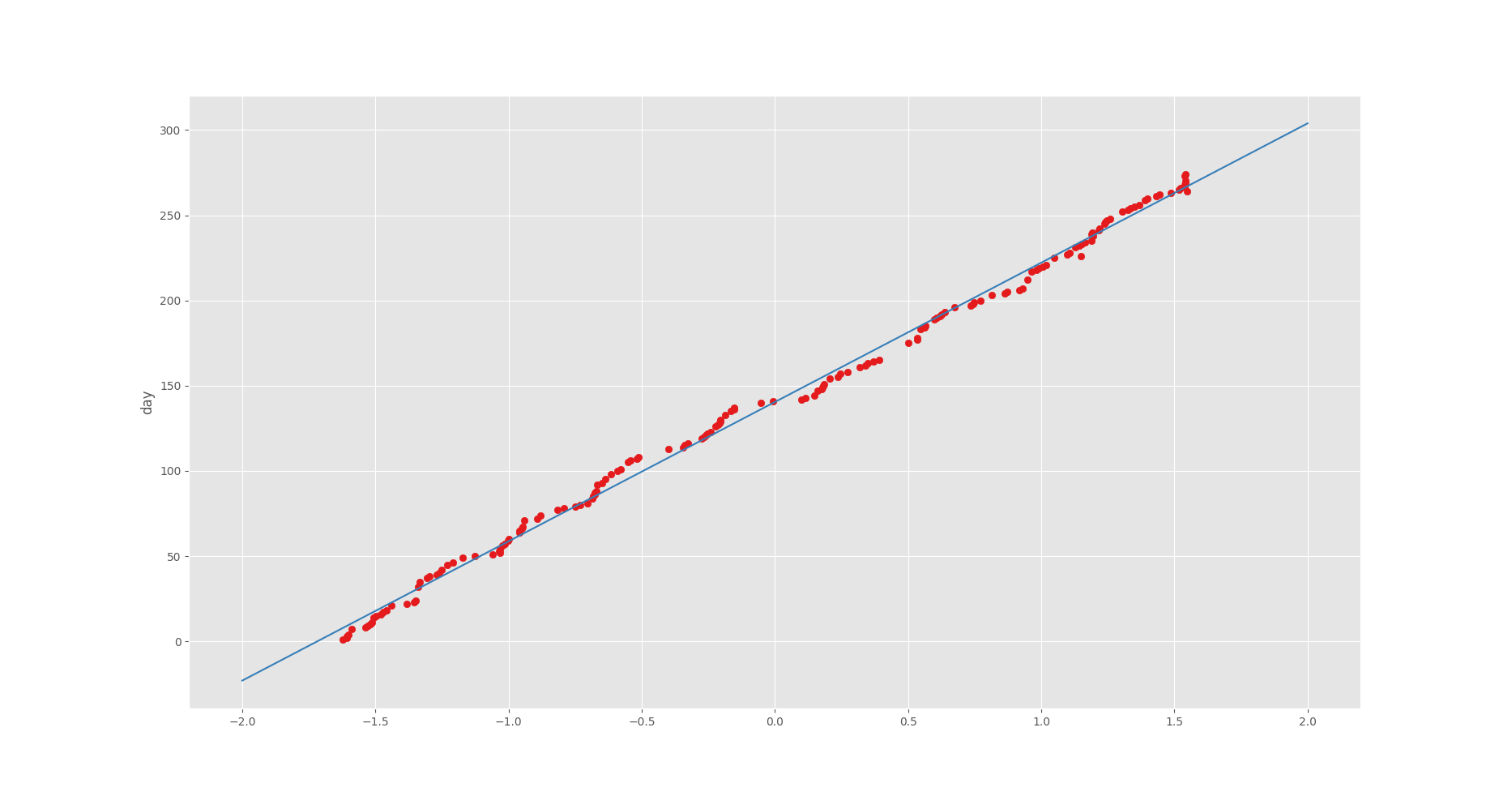
gradient 関数の中で標準出⼒にログを書き出しているので、
学習の様⼦がコンソールから確認できます。
だんだんと前回との誤差の差分が⼩さくなっていく様⼦が⾒て取れますね。
また、勾配法でも最⼩⼆乗法と同じ⽇数が表⽰されています。
出⼒されたグラフも、最⼩⼆乗法との違いがわからないですね。
異なるのは軸の表記くらいでしょうか。
標準化しているため、このような値になります。
6. まとめ
最小二乗法では、方程式を解くことによりパラメータの解析解を求めることで
回帰直線を得ることができました。
また勾配法では、パラメータの学習によって数値解を求めることで
回帰直線を得ることができました。
どちらの手法でも求めていた結果を得ることができて良かったです。
こうやって実際に手を動かして、目に見える結果が得られるのは楽しいですね。
しかし、今回の内容はまだまだ機械学習の序章に過ぎないので、
これからさらに学習を進めていって、ゆくゆくはディープラーニングに挑戦したいと思います。
参考
問い合わせ

サン・エム・システム サービス